As a group of EAGE members and volunteers, the EAGE A.I. Committee is dedicated to helping you navigate the digital world and finding the bits that are most relevant to geoscientists.
You are welcome to join EAGE or renew your membership to support the work of the EAGE A.I. Community and access all the benefits offered by the Association.
EAGE Membership Benefits: Join or Renew
Curious to know all EAGE is doing for the digital transformation?
Visit the EAGE Digitalization Hub
![]()
AI in Subsurface Numerical Modelling: An Overview / Part 2
By Cédric M. John
Last month we have seen that we can use generative models such as GANs to produce realistic-looking volumes of subsurface geology, such as for instance generated pore volumes. In the second (and final) part of this Newsletter, we will explore more advanced techniques that open up the field of process modelling using AI.
![]()
Uncertainty Estimates Using Reduced Order Models (‘Surrogate Models’)
So how can we build on the geostatistical approach of GANs, and generate realistic realization of numerical simulations using machine learning? One potential solution to the problem given a few (100’s) existing numerical simulation results and their inputs is to use surrogate models (such as Bayesian models). But because these surrogate models do not scale well to higher dimensionalities, this is often preceded by a step of reducing dimensionality, i.e. to produce a ‘reduced order models’. Reducing the parameter space (i.e. the number of inputs for the computation) can be done through either linear methods such as Principal Component Analysis (keeping only a few principal components), or via non-linear methods such as t-SNE, embedding, etc… A Bayesian reduced order model approach was taken by Zhu et al (2018, Figure 3) using Convolutional Neural Networks to predict CO2 storage in the subsurface. Once the model is trained, the surrogate Bayesian model can be used to sample arbitrary number of realizations from the latent space, thus hopefully accounting for uncertainties in the subsurface geology.
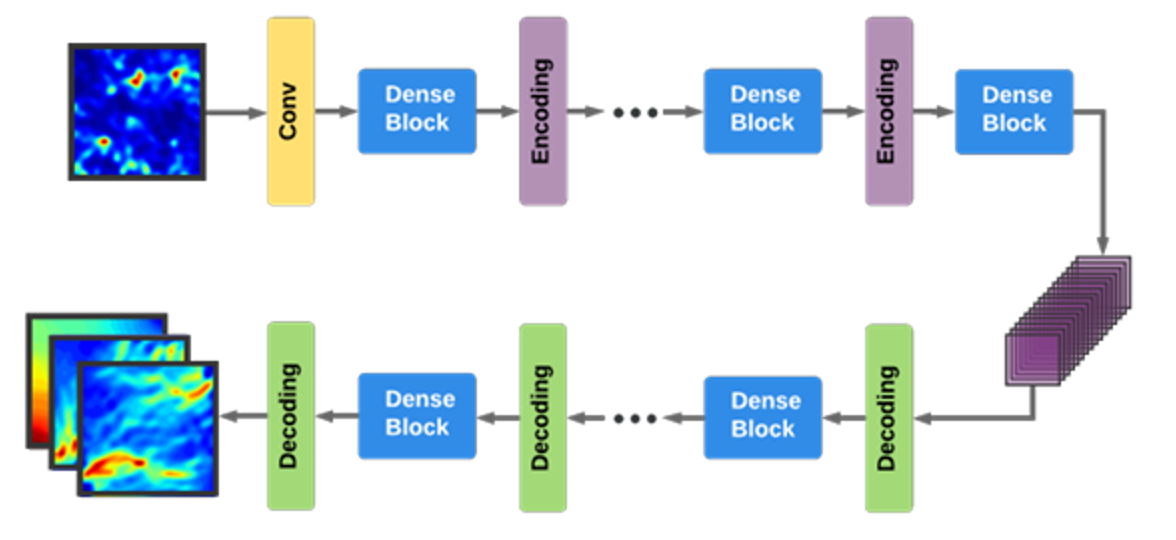
Figure 3: Example of how reduced order modelling and CNN-based Encoder-decoder can be used to generate multi-realisation of a simulation using only few input models. Source: Yinhao Zhu, Nicholas Zabaras, 2018, Bayesian Deep Convolutional Encoder-Decoder Networks for Surrogate Modeling and Uncertainty Quantification
Variations of this approach are popular for subsurface applications at the moment. For instance, CO2 sequestration and plume propagation has been tackled with different flavors of CNN encoder-decoders (see Wen et al, 2021), or with more complex architectures better adapted to this task (Wen et al, 2022). Similar approaches are also used in other fields, such as modelling airflow around building to monitor air pollution (Wu et al, 2020).
![]()
![]()
Towards A full Replacement for Numerical Models: Physics-Informed Neural Networks (PINNs)
The approaches highlighted above learn from the statistical distribution of data, and will generate new model realization that conform to the statistical representation of the train set. However, these models, unlike the numerical forward models that compute partial differential equations, do not incorporate any notion of physics. So, although they are useful, the data-driven models dont always generalize well to other problems, and they can sometimes produce results that are statistically correct, but physically impossible.
So the question is, how could we take advantage of the high-speed inference from deep-learning, but still obtain physically realistic realizations of each timestep of our model? The current answer to this question is to use Physics-Informed Neural Networks (PINNs, Figure 4).
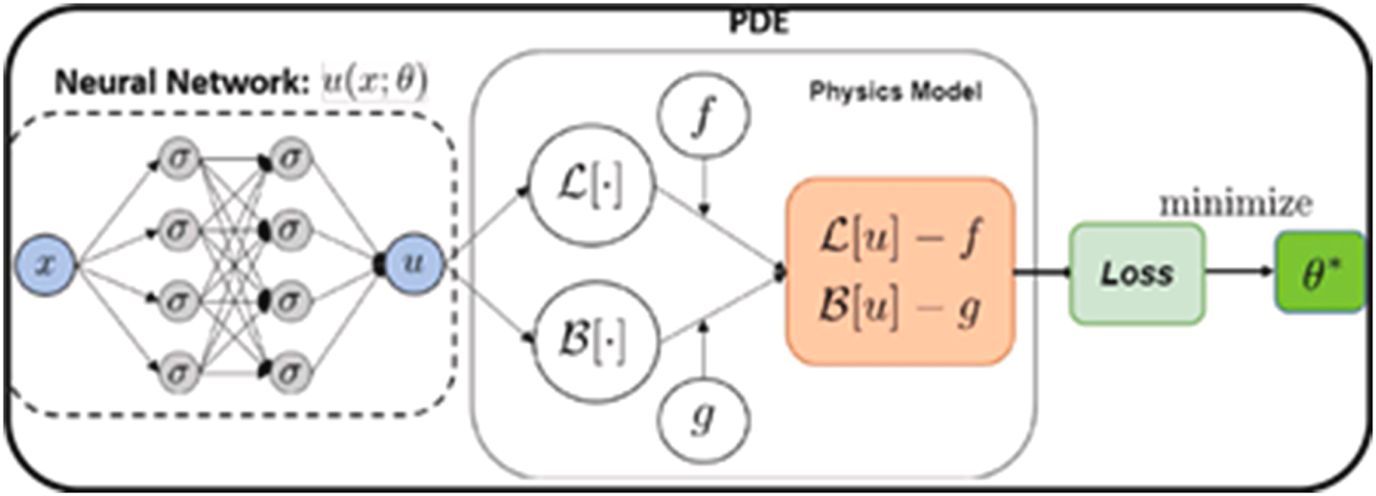
Figure 4: Principle of a Physics-Informed Neural Network (PINN): the loss function is calculated against a full-physics partial differential equation (PDE). Hence, in the process the neural network learns to emulate the simulation code, and can generate results orders of magnitude faster than solving the original PDE. Source: Shashank Reddy Vadyala, Sai Nethra Betgeri, John C. Matthews, Elizabeth Matthews, (2022), A review of physics-based machine learning in civil engineering, Results in Engineering Volume 13, March 2022, 100316
To understand PINNs you need to remember that machine learning models learn by propagating backward the error made at each iteration. This error, also known as a loss, is usually simply computed as the difference between the solution of the train set, and the prediction. For images for instance (a format similar to most geological model outputs), the loss can simply be the mean squared error between each pixels in the train set and the corresponding pixel in the predictions.
The trick with physics-informed Neural Network is to add the actual physics model as part of the loss function. In other words, at each time step, the neural network solution is computed, and is compared against the actual numerical solution from physics. In plain terms, this means that at each training cycle (or epoch) of our neural network, not only do we calculate the new solution for each training instance for the neural network, but we also do the explicit physics modelling. As one can imagine, this is a very slow process, and thus training PINNs is extremely computationally demanding. But the reward is that once trained, the PINNs model is able to compute a solution that is nearly indistinguishable from a physics-based numerical model. And the times to compute a PINNs solution is 3-4 orders of magnitude lower than for the actual numerical model!
PINNs are being used more and more frequently to replace computational fluid dynamic (CFDs) equations. Fluids have a large role in Earth system process, and thus by extension PINNs are used in many fields relevant to the Earth sciences. For instance, ocean modelling and related uncertainties can be done using this method (Lütjens et al, 2021, Wolf et al 2021). PINNs are also finding their ways in other areas of Earth Sciences: Rascht-Behescht (2022) use PINNs for full-waveform inversion of seismic data, for instance.
![]()
Conclusions
As you hopefully grasp from this two-parts newsletter, data-driven modelling is a brand new field with many promising subsurface applications. Because it is a relatively young field, researchers are still testing novel ideas, and evaluating the promises and limitations of established methodologies. Watch this space!
![]()
Catch up with Part 1 of this newsletter here.
We are approaching the EAGE Annual, where a number of digital pathways are ready for you! Take a look at some of the initiatives that you will find in Vienna:
- EAGE Hackathon organized by our AI Committee: this year’s theme is NLP!
- Dedicated Session “Going Big – Scaling Machine Learning Applications in Geoscience and Engineering”: check the Technical Programme Schedule for this and other interesting sessions
- “Interpretation Terminator: Rise of the Machines?“: discover this and other activities at the EAGE Community Hub
- “Geostatistics and its Latest Developments Using Machine Learning Methods“: add a workshop to your EAGE Annual experience
And if you are looking for more opportunities in the world of digitalization, here are some of the next projects you can join via EAGE:
- Machine Learning in Geosciences, an interactive online short course by Gerard Schuster (University of Utah) starting on 9 August
- Seventh EAGE High Performance Computing Workshop: the call for abstracts is open until 20 May
- EAGE Workshop on Data Science – From Fundamentals to Opportunities: you can submit your work until 28 May
This newsletter is edited by the EAGE A.I. Committee.
| Name | Company / Institution | Country |
|---|---|---|
| Anna Dubovik | WAIW | United Arab Emirates |
| Jan H. van de Mortel | Independent | Netherlands |
| Jing Sun | TU Delft | Netherlands |
| Julio Cárdenas | Géolithe | France |
| George Ghon | Capgemini | Norway |
| Lukas Mosser | Aker BP | Norway |
| Oleg Ovcharenko | NVIDIA | United Arab Emirates |
| Nicole Grobys | DGMK | Germany |
| Roderick Perez | OMV | Austria |
| Surender Manral | Schlumberger | Norway |






